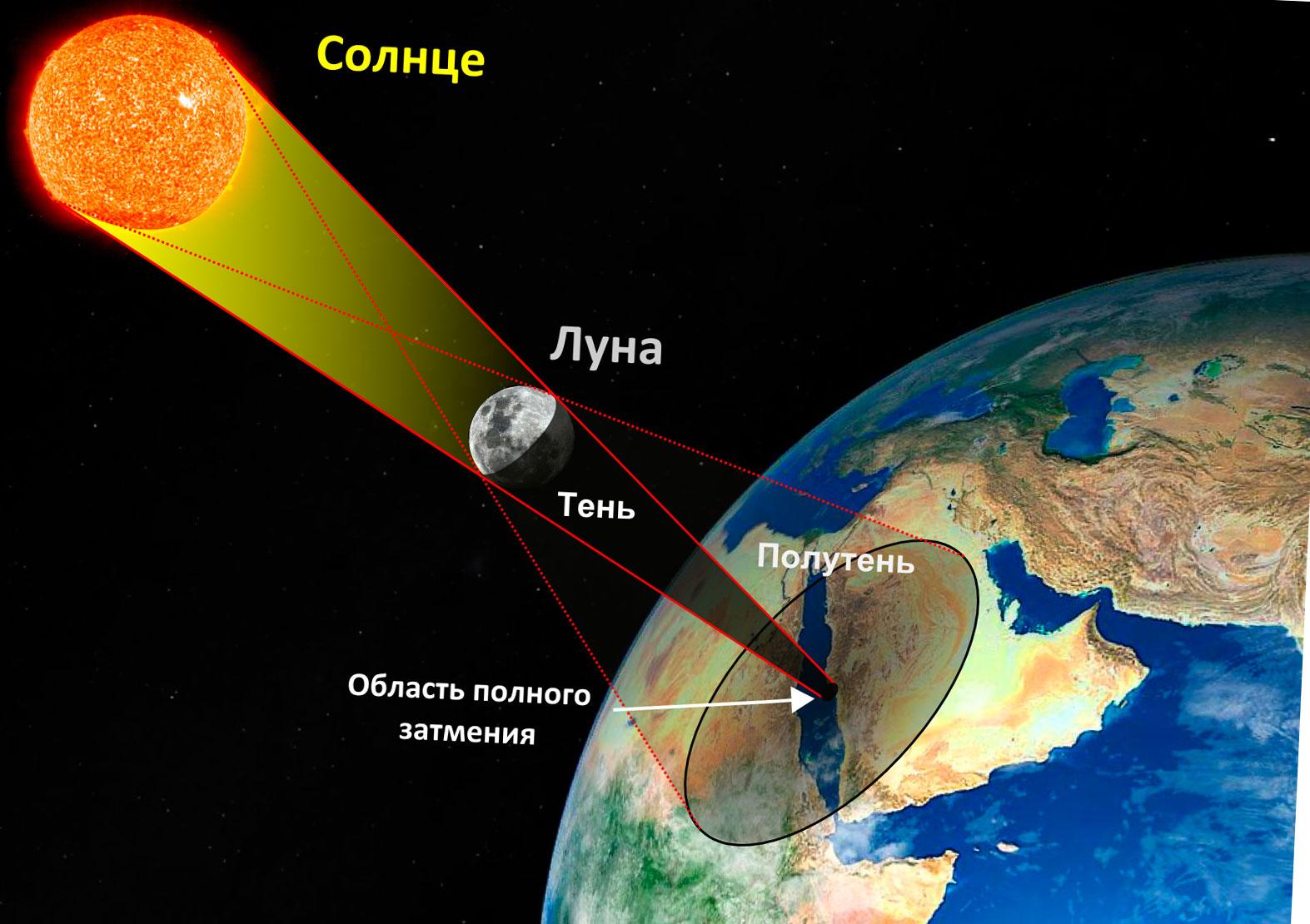
ရောင်စုံစတုရန်းများနှင့် နေလကြတ်များ

ဆောင်းပါးသည် အမျိုးသားကလေးများရန်ပုံငွေအဖွဲ့၏ ပညာသင်ဆုရရှိသူများအတွက် အလယ်တန်းကျောင်းသားများအတွက် ကျွန်ုပ်၏အတန်းများကို ဖော်ပြထားပါသည်။ ဖောင်ဒေးရှင်းသည် အထူးသဖြင့် ထူးချွန်သော ကလေးများနှင့် လူငယ် (မူလတန်းကျောင်းမှ အထက်တန်းကျောင်းအထိ) XNUMX တန်းအထိ ရှာဖွေပြီး ရွေးချယ်ထားသော ကျောင်းသားများကို "ပညာသင်ဆုများ" ပေးပါသည်။ သို့သော်၊ ၎င်းတို့သည် ငွေထုတ်ယူရာတွင် လုံးဝမပါဝင်သော်လည်း စည်းကမ်းအရ နှစ်ပေါင်းများစွာအတွင်း အရည်အချင်းများ ဖွံ့ဖြိုးတိုးတက်မှုအတွက် ပြည့်စုံသောစောင့်ရှောက်မှုတွင် ပါဝင်ပါသည်။ ဤအမျိုးအစား၏အခြားပရောဂျက်များစွာနှင့်မတူဘဲ၊ လူသိများသောသိပ္ပံပညာရှင်များ၊ ယဉ်ကျေးမှုဆိုင်ရာပုဂ္ဂိုလ်များ၊ ထင်ရှားသောလူသားဝါဒီများနှင့် အခြားပညာရှိပုဂ္ဂိုလ်များအပြင် နိုင်ငံရေးသမားအချို့သည် ဖောင်ဒေးရှင်း၏ရပ်ကွက်များကို အလေးအနက်ထားကြသည်။

ဖောင်ဒေးရှင်း၏ လှုပ်ရှားမှုများသည် အားကစားအပါအဝင် အခြေခံကျောင်း ဘာသာရပ်များဖြစ်သည့် ဘာသာရပ်အားလုံးတွင် အကျုံးဝင်ပါသည်။ ရန်ပုံငွေကို ထိုအချိန်က အဖြစ်မှန်အတွက် ဖြေဆေးအဖြစ် 1983 ခုနှစ်တွင် ဖန်တီးခဲ့သည်။ မည်သူမဆို ရန်ပုံငွေသို့ လျှောက်ထားနိုင်သည် (များသောအားဖြင့် ကျောင်းတစ်ကျောင်းမှတဆင့် ဖြစ်နိုင်ရင် စာသင်နှစ်မကုန်မီ)၊ သို့သော်၊ သေချာသည်မှာ၊ အချို့သော ဆန်ခါ၊ အရည်အချင်းစစ် လုပ်ထုံးလုပ်နည်းတစ်ခု ရှိပါသည်။

ကျွန်တော်ပြောပြီးသားအတိုင်း၊ ဆောင်းပါးသည် III အထက်တန်းကျောင်းရှိ 2016th အငယ်တန်းအထက်တန်းကျောင်းတွင် 24 ခုနှစ်မတ်လတွင် Gdynia တွင်အထူးသဖြင့်ကျွန်ုပ်၏မာစတာအတန်းများကိုအခြေခံထားသည်။ ရေတပ်။ နှစ်ပေါင်းများစွာကြာအောင် ဤနှီးနှောဖလှယ်ပွဲများကို ဖောင်ဒေးရှင်း၏ ပံ့ပိုးကူညီမှုအောက်တွင် ထူးထူးခြားခြား ဆွဲဆောင်မှုရှိပြီး ဥာဏ်ရည်မြင့်မားသော ဆရာ Wojciech Thomalczyk မှ စီစဉ်ပေးခဲ့ပါသည်။ 2008 ခုနှစ်တွင်သူသည် Pedagogy ပါမောက္ခဘွဲ့ (လွန်ခဲ့သောနှစ်ပေါင်းများစွာကပေးဆောင်သောဥပဒေ) မှချီးမြှင့်ခံရသောပိုလန်တွင်ထိပ်တန်းဆယ်ယောက်တွင်ဝင်ရောက်ခဲ့သည်။ "ပညာရေးသည် ကမ္ဘာ၏ဝင်ရိုးဖြစ်သည်" ဟူသော ကြေညာချက်တွင် အနည်းငယ်ချဲ့ကားဖော်ပြထားသည်။

လ အမြဲတမ်း စွဲမက်ဖွယ်ကောင်းသည် - ထို့နောက် အရာခပ်သိမ်းသည် စင်တီမီတာနှင့် စက္ကန့်တိုင်း ရွေ့လျားနေသည့် ကြီးမားလှသော အာကာသအတွင်းတွင် ကျွန်ုပ်တို့နေထိုင်သည့် ဂြိုဟ်ငယ်လေးပေါ်တွင် သင်ခံစားနိုင်သည်။ အဲဒါက ကျွန်မကို နည်းနည်းလေးတောင် ကြောက်စရာကောင်းတယ်၊ အချိန်အမြင်လည်းရှိတယ်။ ယနေ့ ဝါဆောဒေသမှ မြင်ရသော နေကြတ်မည့် စုစုပေါင်း နေကြတ်မှုသည် ... 2681 တွင် ဖြစ်မည် ဖြစ်ကြောင်း ကျွန်ုပ်တို့ လေ့လာသိရှိရပါသည်။ ဘယ်သူတွေ့မှာလဲလို့ တွေးမိတယ်။ ကျွန်ုပ်တို့၏ကောင်းကင်ရှိ နေနှင့်လ၏ ထင်ရှားသောအရွယ်အစားမှာ တူညီလုနီးပါးဖြစ်သည်- ထို့ကြောင့် လကြတ်ခြင်းများသည် အလွန်တိုတောင်းပြီး အလွန်အံ့မခန်းလှပါသည်။ ရာစုနှစ်များစွာကြာအောင်၊ ထိုမိနစ်တိုတိုသည် နေရောင်ခြည်ကိုရိုနာကို မြင်နိုင်ရန် နက္ခတ္တဗေဒပညာရှင်များအတွက် လုံလောက်သင့်သည်။ တစ်နှစ်မှာ နှစ်ကြိမ် ဖြစ်ပွားတာ ထူးဆန်းတယ်...ဒါပေမယ့် ကမ္ဘာပေါ်က တစ်နေရာရာမှာ အချိန်တိုတိုလေးပဲ မြင်နိုင်မယ်လို့ ဆိုလိုတာပါ။ ဒီရေရွေ့လျားမှုကြောင့် လသည် ကမ္ဘာမှ ဝေးကွာသွားသည် - နှစ်သန်းပေါင်း 260 တွင် ကျွန်ုပ်တို့ (ကျွန်ုပ်တို့) သည် အဝိုင်းနေကြတ်ခြင်းကိုသာ မြင်နိုင်မည်ဖြစ်သည်။

ကြိုတင်ဟောကိန်းထုတ်ရန် ထင်ရှားပါသည်။ နေကြတ်ခြင်း။Thales of Miletus (BC 28-585 ရာစုနှစ်များ)။ အာရှမိုင်းနားတွင် နေကြတ်ခြင်းသည် မေလ ၅၆၇၊ ၅၆၆ BC တွင် ခေတ်သစ်တွက်ချက်မှုများဖြင့် အတည်ပြုထားသည့်အချက်ဖြစ်သောကြောင့် အမှန်တကယ်ဖြစ်ပျက်ခြင်းရှိ၊ မရှိ ကျွန်ုပ်တို့မသိနိုင်ပေ။ ဟုတ်ပါတယ်၊ ဒီနေ့ခေတ်အချိန်အကောင့်အတွက် အချက်အလက်တွေကို ကိုးကားပါတယ်။ ငယ်ငယ်တုန်းက လူတွေက နှစ်တွေကို ဘယ်လိုရေတွက်ကြလဲ တွေးကြည့်တယ်။ ထို့ကြောင့်၊ ဤသည်မှာ၊ ဥပမာအားဖြင့် 567 BC၊ နှစ်သစ်ကူးအကြိုရောက်လာတော့မည်၊ လူများဝမ်းမြောက်နေကြသည်- ဘီစီ ကိုးနှစ်သာ။ “ငါတို့ခေတ်” နောက်ဆုံးတော့ ရောက်လာတဲ့အခါ သူတို့ ဘယ်လောက်ပျော်ကြမလဲ။ လွန်ခဲ့သောနှစ်အနည်းငယ်က ကျွန်ုပ်တို့ကြုံတွေ့ခဲ့ရသည့် ထောင်စုနှစ်အလှည့်အပြောင်းတစ်ခုဖြစ်သည်။

ရက်စွဲများနှင့် အပိုင်းအခြားများ တွက်ချက်ခြင်း သင်္ချာ နေကြတ်ခြင်း၊အထူးရှုပ်ထွေးခြင်းမရှိသော်လည်း ပုံမှန်ဖြစ်တည်မှုနှင့် ဆက်နွှယ်သည့်အချက်မျိုးစုံဖြင့် ပြည့်ကျပ်နေပြီး၊ ပိုဆိုးသည်မှာ ပတ်လမ်းများတွင် ခန္ဓာကိုယ်၏မညီမညာလှုပ်ရှားမှုများနှင့် ပိုဆိုးသည်။ ဒီသင်္ချာကိုတောင် သိချင်ပါတယ်။ Thales of Miletus သည် လိုအပ်သော တွက်ချက်မှုများကို မည်သို့ပြုလုပ်နိုင်မည်နည်း။ အဖြေက ရိုးရှင်းပါတယ်။ ကောင်းကင်မြေပုံရှိရမည်။ ဒီလိုမြေပုံကို ဘယ်လိုဖန်တီးမလဲ။ ဒါကလည်း မခက်ပါဘူး၊ ရှေးခေတ်အီဂျစ်လူမျိုးတွေက ဒါကို ဘယ်လိုလုပ်ရမလဲ။ သန်းခေါင်ယံအချိန်၌ ဘုန်းကြီးနှစ်ပါးသည် ဗိမာန်တော်ခေါင်မိုးပေါ်သို့ ထွက်လာကြသည်။ တစ်ယောက်ချင်းစီ ထိုင်ပြီး သူမြင်တာကို (သူ့လုပ်ဖော်ကိုင်ဖက်လို) ဆွဲတယ်။ အနှစ်နှစ်ထောင်ကျော်ကြာတော့ ဂြိုလ်တွေရဲ့ ရွေ့လျားမှုအကြောင်းကို အားလုံးသိကြပါတယ်..။

လှပသော ဂျီသြမေတြီ သို့မဟုတ် "ကော်ဇော" ပေါ်တွင် ပျော်စရာ၊

ဂရိလူမျိုးများသည် ဂဏန်းများကို မကြိုက်ကြဘဲ ဂျီသြမေတြီကို အသုံးပြုကြသည်။ ဒါကငါတို့ဘာလုပ်မလဲ။ ကျွန်တော်တို့ရဲ့ နေကြတ်ခြင်း။ ၎င်းတို့သည် ရိုးရိုးရှင်းရှင်း၊ အရောင်အသွေးစုံသော်လည်း စိတ်ဝင်စားစရာကောင်းပြီး အစစ်အမှန်ဖြစ်လိမ့်မည်။ အပြာရောင်ရုပ်သည် အနီရောင်ကို ကြတ်စေသည့်ပုံစံဖြင့် ရွေ့လျားနေသည့် ကွန်ဗင်းရှင်းကို လက်ခံပါသည်။ အပြာရောင်ရုပ်ကို လ၊ အနီရောင်ရုပ်ကို နေကို ခေါ်ကြပါစို့။ ကျွန်ုပ်တို့သည် မိမိကိုယ်ကို အောက်ပါမေးခွန်းများကို မေးသည်-

1. နေကြတ်တာ ဘယ်လောက်ကြာလဲ။
2. ပစ်မှတ်တစ်ဝက်ကို ဖုံးလွှမ်းသွားသောအခါ၊

   ထမင်း။ 1 နေနှင့်လနှင့်အတူရောင်စုံ "ကော်ဇော"

3. အမြင့်ဆုံးလွှမ်းခြုံမှုကား အဘယ်နည်း။
4. ဒိုင်းဖုံးလွှမ်းမှုအပေါ် အချိန်မီ ခွဲခြမ်းစိတ်ဖြာရန် ဖြစ်နိုင်ပါသလား။ ဤဆောင်းပါးတွင် (စာသားပမာဏကန့်သတ်ထားသည်) ဒုတိယမေးခွန်းကို ကျွန်ုပ်အာရုံစိုက်ပါမည်။ ဤအရာ၏နောက်ကွယ်တွင် ပျင်းစရာကောင်းသော တွက်ချက်မှုများမပါဘဲ ဖြစ်ကောင်းဖြစ်နိုင်သည့် ဂျီသြမေတြီတစ်ခုဖြစ်သည်။ သဖန်းသီးကို ကြည့်ရအောင်။ ၁။ နေကြတ်ခြင်းနဲ့ ဆက်စပ်နေတယ်လို့ ယူဆနိုင်ပါသလား။

ကျွန်တော်ဆွေးနွေးမယ့် အလုပ်တွေကို အလယ်တန်းနဲ့ အထက်တန်း ကျောင်းသားတွေရဲ့ အသိပညာနဲ့ ကျွမ်းကျင်မှုတွေနဲ့ လိုက်လျောညီထွေဖြစ်အောင် အထူးရွေးချယ်သွားမှာ ဖြစ်တယ်လို့ ရိုးရိုးသားသား ပြောရပါမယ်။ ဒါပေမယ့် ဂီတသမားတွေက စကေးတွေတီးတဲ့ အလုပ်တွေကို လေ့ကျင့်ပေးပြီး အားကစားသမားတွေဟာ အထွေထွေ ဖွံ့ဖြိုးမှုဆိုင်ရာ လေ့ကျင့်ခန်းတွေ လုပ်ကြပါတယ်။ ထို့အပြင်၊ ၎င်းသည် လှပသော ကော်ဇော (ပုံ ၁) မျှသာ မဟုတ်လော။

ထမင်း။ 2 "အပြာ" လနှင့် "အနီရောင်" နေ

ကျွန်ုပ်တို့၏ ကောင်းကင်ခန္ဓာများသည် အနည်းဆုံး အစပိုင်းတွင် ရောင်စုံစတုရန်းများ ဖြစ်လိမ့်မည်။ လသည် အပြာ၊ နေသည် အနီရောင် (အရောင်ခြယ်ရန် အကောင်းဆုံး)။ ပစ္စုပ္ပန်နှင့်အတူ နေကြတ်ခြင်း။ လသည် ကောင်းကင်ကို ဖြတ်၍ နေကို ဖမ်းယူ၍ ပိတ်သည်။ ငါတို့နဲ့အတူတူပဲဖြစ်လိမ့်မယ်။ ပုံတွင်ပြထားသည့်အတိုင်း လသည် နေနှင့် နှိုင်းယှဉ်ပါက အရိုးရှင်းဆုံးကိစ္စဖြစ်သည်။ 2. လ၏ဒစ်အစွန်းသည် နေ၏ဒစ်အစွန်း (ပုံ 2) ကိုထိသောအခါ နေကြတ်ခြင်းအစပြုကာ ၎င်းကိုကျော်လွန်သွားသောအခါတွင် ကုန်ဆုံးသည်။

ထမင်း။ ၃ လသည် နေကို ထောင့်ဖြတ်ချဉ်းကပ်သည်။

"လ" သည် အချိန်ယူနစ်တစ်ခုလျှင် ဥပမာအားဖြင့် တစ်မိနစ်လျှင် ဆဲလ်တစ်ခု ရွေ့လျားသည်ဟု ကျွန်ုပ်တို့ ယူဆသည်။ ထို့နောက် နေကြတ်ခြင်းသည် အချိန် ရှစ်ယူနစ် ကြာပြီး မိနစ်ဟု ဆိုနိုင်ပါသည်။ တစ်ဝက် နေကြတ်ခြင်း။ လုံးဝမှိန်သွားသည် ဒိုင်ခွက်တစ်ဝက်ကို နှစ်ကြိမ်ပိတ်သည်- 2 နှင့် 6 မိနစ်အကြာတွင်။ ရာခိုင်နှုန်း အနှောင့်အယှက်ပေးသည့် ဂရပ်သည် ရိုးရှင်းသည်။ ပထမနှစ်မိနစ်အတွင်း၊ ဒိုင်းသည် သုညမှ 1 နှုန်းဖြင့် အညီအမျှပိတ်သည်၊ နောက်နှစ်မိနစ်တွင် ၎င်းကို တူညီသောနှုန်းဖြင့် ထိတွေ့သည်။

ဤတွင် ပိုစိတ်ဝင်စားစရာကောင်းသော ဥပမာတစ်ခု (ပုံ။ 3)။ လသည် နေကို ထောင့်ဖြတ် ချဉ်းကပ်သည်။ ကျွန်ုပ်တို့၏ တစ်မိနစ် ငွေပေးချေမှု သဘောတူညီချက်အရ နေကြတ်ခြင်းသည် 8√ ကြာမြင့်သည်။2 မိနစ် - ဤအချိန်အလယ်တွင် ကျွန်ုပ်တို့တွင် စုစုပေါင်းနေကြတ်ခြင်းရှိသည်။ အချိန်ပြီးနောက် နေ၏ မည်သည့်အပိုင်းကို ဖုံးလွှမ်းထားသည်ကို တွက်ချက်ကြည့်ရအောင် (ပုံ ၃)။ နေကြတ်ခြင်းအစကတည်းက t မိနစ်များကျော်လွန်သွားပါက၊ ထို့ကြောင့် လသည် ပုံတွင်ပြထားသည့်အတိုင်းဖြစ်သည်။ 3၊ ထို့နောက် (သတိထား!) ထို့ကြောင့်၊ ၎င်းသည် (စတုရန်း APQR ဧရိယာ) ကို ဆိုလာဒစ်တစ်ဝက်နှင့် ညီမျှသည်၊ ထို့ကြောင့် ၎င်းကို ဖုံးအုပ်ထားသည့်အခါ၊ ဆိုလိုသည်မှာ၊ 5 မိနစ်ပြီးနောက် (ထို့နောက် နေကြတ်ခြင်းမပြီးဆုံးမီ 4 မိနစ်)။

ထမင်း။ 4 "shading" လုပ်ဆောင်ချက်၏ဂရပ်

ကြတ်ခြင်း။ တစ်ခဏကြာသည် (t = 4√2) နှင့် "shaded part" function ၏ ဂရပ်သည် parabolas နှစ်ခုပါ၀င်သည် (ပုံ။ 4)။

ကျွန်ုပ်တို့၏ အပြာရောင်လသည် အနီရောင်နေဖြင့် ထောင့်စွန်းကိုထိလိမ့်မည်၊ သို့သော် ၎င်းကို ထောင့်ဖြတ်မဟုတ်ဘဲ အနည်းငယ် ထောင့်ဖြတ်ဖြင့် ဖုံးအုပ်သွားမည်ဖြစ်သည်။ စိတ်လှုပ်ရှားမှု အနည်းငယ် ရှုပ်ထွေးလာသောအခါတွင် စိတ်ဝင်စားဖွယ်ကောင်းသော ဂျီသြမေတြီ ပေါ်လာသည် (ပုံ ၆)။ ရွေ့လျားမှု၏ဦးတည်ချက်သည် ယခုအခါ vector [6] ဖြစ်သည်၊ ဆိုလိုသည်မှာ "ညာဘက်တွင် ဆဲလ်လေးခု၊ ဆဲလ်သုံးဆဲလ်အပေါ်သို့" ဖြစ်သည်။ နေ၏ အနေအထားသည် နေကြတ်ခြင်း (အနေအထား A) ၏ အလျား လေးပုံတစ်ပုံသို့ ရောက်ရှိလာသောအခါတွင် နေကြတ်ခြင်း စတင်ခြင်း ဖြစ်သည်။ လသည် B အနေအထားသို့ ရွေ့လျားသောအခါ နေ၏ ခြောက်ပုံတစ်ပုံ နေကြတ်မည်ဖြစ်ပြီး အနေအထား C တွင် တစ်ဝက်နေမှ နေကြတ်မည်ဖြစ်သည်။ အနေအထား D တွင်၊ ကျွန်ုပ်တို့တွင် စုစုပေါင်းနေကြတ်ခြင်းရှိပြီး၊ ထို့နောက် အရာအားလုံးသည် "အရင်အတိုင်း" ပြန်သွားပါသည်။

ထမင်း။ 5 အချိန်အတွင်း ဝှက်ထားသော နေ၏ အစိတ်အပိုင်း

လသည် G အနေအထားတွင် ရှိနေသောအခါတွင် နေကြတ်ခြင်းမှာ ကုန်ဆုံးပါသည်။ အပိုင်းအရှည် AG. ယခင်ကကဲ့သို့၊ လသည် "တစ်စတုရန်း" ဖြတ်သန်းသည့်အချိန်ကို အချိန်ယူနစ်အဖြစ်ယူပါက AG ၏အလျားသည် ညီမျှသည်။ အကယ်၍ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ ကောင်းကင်ကိုယ်ခန္ဓာသည် 4 နှင့် 4 ဖြစ်သည်ဟူသော စည်းဝေးကြီးဟောင်းသို့ ပြန်သွားပါက ရလဒ်သည် ကွဲပြားလိမ့်မည် (ဘာလဲ။) ပြသရန်လွယ်ကူသောကြောင့် ပစ်မှတ်သည် t < 15 ပြီးနောက် ပိတ်သွားပါသည်။ "မျက်နှာပြင်လွှမ်းခြုံမှုရာခိုင်နှုန်း" လုပ်ဆောင်ချက်၏ ဂရပ်ကို ပုံတွင် မြင်တွေ့နိုင်ပါသည်။ ၆။

ထမင်း။ "ရာခိုင်နှုန်းကာကွယ်မှု" လုပ်ဆောင်ချက်၏ 6 ဂရပ်

နေကြတ်ခြင်းနှင့် ခုန်ခြင်း ညီမျှခြင်း

ထမင်း။ 7 ပုံတွင်ပြထားသည့် နေကြတ်ချိန်အတွင်း ဆိုလာဒစ်ကို အဟန့်အတားဖြစ်စေသည်။ ၆

စက်ဝိုင်းကိစ္စ မစဉ်းစားပါက လကြတ်ခြင်းပြဿနာသည် မပြည့်စုံပါ။ ဒါက ပိုရှုပ်ထွေးပါတယ်၊ ဒါပေမယ့် စက်ဝိုင်းတစ်ခုက တခြားတစ်ဝက်ကို နေကြတ်တဲ့အခါ၊ နှစ်ခုလုံးကို ချိတ်ဆက်ထားတဲ့ အချင်းတစ်လျှောက် ရွေ့သွားတဲ့အခါ အရိုးရှင်းဆုံး အခြေအနေမှာ၊ အရိုးရှင်းဆုံးအနေနဲ့၊ ပုံသည် အချို့သော ခရက်ဒစ်ကတ်ကိုင်ဆောင်သူများနှင့် ရင်းနှီးသည်။

အကွက်များ၏ အနေအထားကို တွက်ချက်ရာတွင် ရှုပ်ထွေးသည်၊ ပထမအချက်မှာ စက်ဝိုင်းအပိုင်း၏ ဧရိယာအတွက် ပုံသေနည်းအသိပညာ၊ ဒုတိယအချက်မှာ ထောင့်၏ arc အသိပညာ၊ တတိယအချက်မှာ စွမ်းရည် (အဆိုးဆုံး)၊ အချို့သော jump equation ကိုဖြေရှင်းရန်။ "အကူးအပြောင်းညီမျှခြင်း" က ဘာလဲဆိုတာ မရှင်းပြတော့ပါဘူး၊ ဥပမာ (ပုံ 8) ကိုကြည့်ရအောင်။

ထမင်း။ နေကြတ်ခြင်း ၈ "လုံးပတ်"

စက်ဝိုင်းအပိုင်းသည် မျဉ်းဖြောင့်ဖြင့် စက်ဝိုင်းကိုဖြတ်ပြီးနောက် ကျန်ရှိနေသော "ပန်းကန်" ဖြစ်သည်။ ထိုသို့သောအပိုင်း၏ဧရိယာသည် S = 1/2r ဖြစ်သည်။²(φ-sinφ) ၊ r သည် စက်ဝိုင်း၏ အချင်းဝက်ဖြစ်ပြီး φ သည် အပိုင်းကျိန်းဝပ်သည့် ဗဟိုထောင့်ဖြစ်သည် (ပုံ။ 8)။ ဤသည်မှာ မြို့ပတ်ရထားကဏ္ဍ၏ ဧရိယာမှ တြိဂံ၏ ဧရိယာကို နုတ်ခြင်းဖြင့် အလွယ်တကူ ရရှိနိုင်သည်။

အပိုင်း O₁O₂ (စက်ဝိုင်း၏အလယ်ဗဟိုကြားအကွာအဝေး) သည် 2rcosφ/2 နှင့် ညီမျှပြီး အမြင့် (အနံ၊ “ခါးလိုင်း”) h = 2rsinφ/2။ ထို့ကြောင့် လသည် ဆိုလာဒစ်၏ တစ်ဝက်ကို မည်သည့်အချိန်တွင် ဖုံးလွှမ်းမည်ကို ကျွန်ုပ်တို့ တွက်ချက်လိုပါက ညီမျှခြင်းအား ဖြေရှင်းရန် လိုအပ်သည်- ရိုးရှင်းပြီးနောက် ဖြစ်လာသည်-

ထမင်း။ 9 လုပ်ဆောင်ချက်နှစ်ခု၏ဂရပ်ဖစ်များ

ထိုညီမျှခြင်းများ၏ အဖြေသည် ရိုးရှင်းသော အက္ခရာသင်္ချာထက် ကျော်လွန်သွားသည် - ညီမျှခြင်းတွင် ထောင့်များနှင့် ၎င်းတို့၏ trigonometric လုပ်ဆောင်ချက်များ ပါဝင်ပါသည်။ ညီမျှခြင်းသည် သမားရိုးကျနည်းလမ်းများ၏ လက်လှမ်းမီမှုထက် ကျော်လွန်ပါသည်။ အဲဒါကြောင့် ခေါ်တာ။ ခုန်ရန်. လုပ်ဆောင်ချက်နှစ်ခုလုံး၏ ဂရပ်ဖစ်များကို ကြည့်ကြပါစို့၊ ဆိုလိုသည်မှာ လုပ်ဆောင်ချက်များနှင့် လုပ်ဆောင်ချက်များအား ဤပုံမှ အနီးစပ်ဆုံး အဖြေကို ကျွန်ုပ်တို့ဖတ်ရှုနိုင်ပါသည်။ သို့သော်၊ ကျွန်ုပ်တို့သည် ထပ်ခါတလဲလဲ အနီးစပ်ဆုံးကိုရနိုင်သည် သို့မဟုတ်… Excel ဇယားတွင် Solver ရွေးချယ်မှုကို အသုံးပြုပါ။ 20 ရာစုဖြစ်သောကြောင့် အထက်တန်းကျောင်းသူတိုင်း လုပ်နိုင်သင့်သည်။ ပိုဆန်းပြားတဲ့ Mathematica tool ကိုသုံးခဲ့တယ်၊ ဒါက မလိုအပ်တဲ့ တိကျမှု XNUMX ဒဿမ နေရာတွေနဲ့ ဖြေရှင်းချက်ပါ။

SetPrecision[FindRoot[x==Sin[x]+Pi/2၊{x,2}],20] {x⇒2.3098814600100574523}.

ထမင်း။ matematica တွင် နေကြတ်ခြင်း၏ လှုပ်ရှားသက်ဝင်မှု 10

ကျွန်ုပ်တို့သည် ၎င်းကို 180/π ဖြင့် မြှောက်ခြင်းဖြင့် ဒီဂရီအဖြစ်ပြောင်းသည်။ ကျွန်ုပ်တို့သည် 132 ဒီဂရီ၊ 20 မိနစ်၊ 45 နှင့် arc စက္ကန့်၏လေးပုံတစ်ပုံကိုရရှိသည်။ စက်ဝိုင်း၏ အလယ်ဗဟိုအကွာအဝေးသည် O ဖြစ်သည် ဟု ကျွန်ုပ်တို့ တွက်ချက်ပါသည်။₁O₂ အချင်းဝက် = 0,808 နှင့် "ခါး" 2,310။